
 |  |  |

Equazione del tempo e analemma
Se vi è mai capitato di osservare il quadrante di una meridiana, forse potreste aver notato una linea a forma di "8" che prende il nome di analemma.
Questa linea ha il ruolo di "tradurre" il tempo naturalmente dettato dal sole in quello artificiale che tutti noi siamo abituati a leggere sugli orologi. Il significato e la particolare forma dell'analemma sono strettamente legati al moto della Terra e al concetto di equazione del tempo.
Come è possibile che parametri dell'orbita terrestre possano prendere forma in questa particolare traccia curvilinea? E cosa è l'equazione del tempo?
In questa pagina cercherò di spiegarlo.

Particolare di analemma su una meridiana.
Introduzione
È difficile mostrare su due piedi come si legga l'ora su una meridiana: a volte l'ora che indica il quadrante differisce di decine di minuti da quella dei nostri orologi e sembra che la meridiana sia stata mal costruita. Eppure non è un errore, ma semplicemente una diversità nella definizione di ora: non serve altro che un po' di pratica per capire come "correggere" questo scarto, e con un analemma disegnato sulla meridiana diventa ancora più facile.
Una volta però che si è capito come leggere l'ora, viene naturale chiedersi "Perché?". Perché tanta fatica per leggere l'ora e perché serve una forma tanto strana come quella di un analemma per tradurre la posizione del Sole nell'ora a cui siamo abituati?
Quando ho finito di costruire la mia meridiana, mi sono trovato io stesso a dover rispondere a queste domande che amici, parenti o curiosi mi facevano. Così, poiché non sono argomenti facili, ho deciso di scrivere questa pagina che vuole rispondere al "Perché?" dal quale è immediata anche la risposta al "Come?".
La trattazione su questo argomento è di carattere scientifico e presenta molti termini propri della materia, ma, se corredata da ricerche in merito ad alcune parole o fenomeni che qui nomino solamente, può essere letta e soprattutto capita da chiunque. Se non avete dimestichezza con le coordinate astronomiche o la gravitazione leggete con molta calma il documento: i fenomeni che si affrontano non sono ovvi.
Buona lettura!
L'equazione del tempo
L'equazione del tempo è un valore variabile nel corso dell'anno che esprime la differenza tra il tempo solare vero [1] (quello segnato comunemente dalle linee delle meridiane) e il tempo medio, quello a cui siamo tutti abituati e per il quale ogni giorno dura 24h.
L'equazione del tempo si può rappresentare graficamente in funzione del giorno dell'anno o in funzione della declinazione del Sole. In questo secondo caso la curva così disegnata prende il nome di analemma. Si osservi che ad ogni declinazione generalmente corrispondono due giorni all'anno, ecco perché l'analemma è una curva a "8".
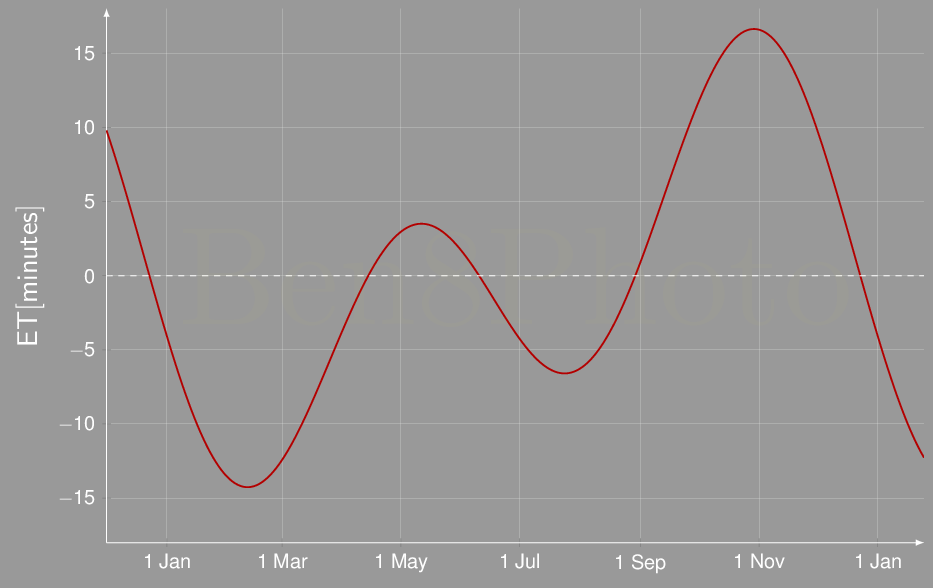
Equazione del tempo in funzione della data
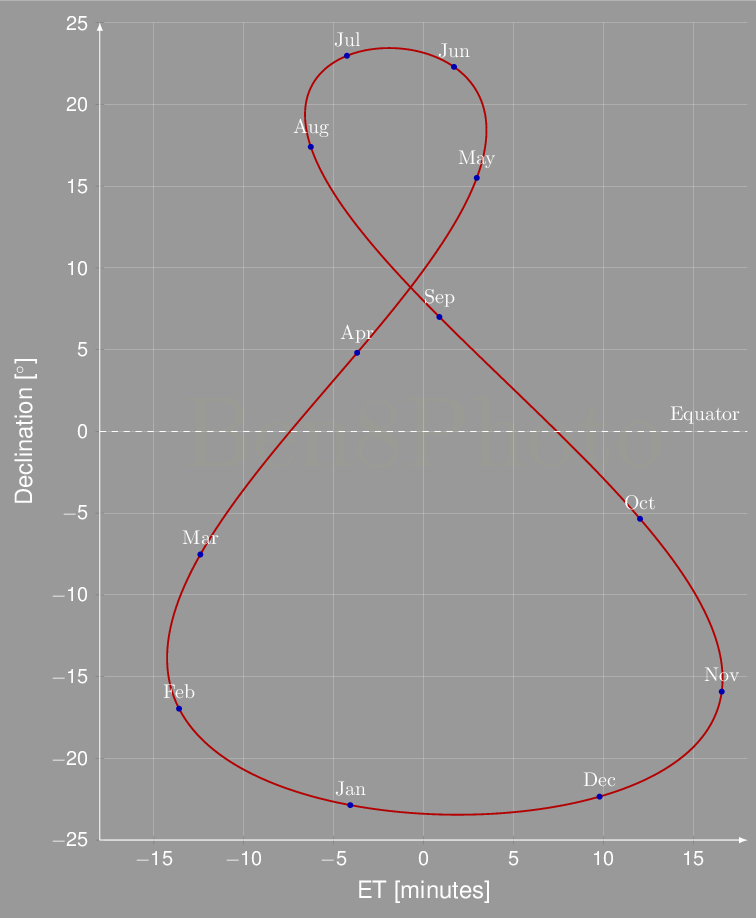
Equazione del tempo in funzione della declinazione
La differenza tra l'ora solare e quella media (ovvero l'equazione del tempo), trascurando effetti su lungo periodo, è diversa da zero a causa di due fenomeni:
- L'eccentricità dell'orbita terrestre, ovvero il fatto che l'orbita della Terra è un'ellisse e non un cerchio perfetto.
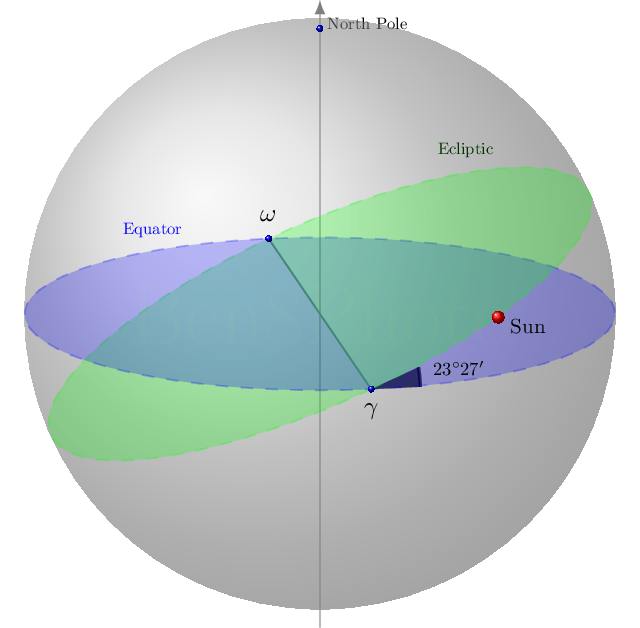
- L'inclinazione del piano dell'eclittica rispetto a quello dell'equatore celeste, quella che viene comunemente indicata come inclinazione dell'asse terrestre e che vale 23° 27'
Ora ci concentreremo separatamente sui due fenomeni per cercare di capire come essi siano coinvolti nel determinare il valore dell'equazione del tempo.
L'eccentricità
L'orbita terrestre è un'ellisse con un'eccentricità pari a ε = 0.0167 dove ε = 0 corrisponde ad un'orbita circolare. Il Sole, come enuncia la prima legge di Keplero, occupa uno dei fuochi di questa ellisse perciò esiste un momento dell'anno in cui la Terra si trova alla minima distanza dal Sole, tale punto è detto Perielio. Dopo metà anno, invece, la Terra si trova all'afelio che è il punto più distante dal Sole.
Per la seconda legge di Keplero la velocità angolare della Terra lungo l'orbita non è costante (quella conservata è la velocità areolare) perciò anche il moto apparente del Sole visto dalla Terra ha velocità [2] non costante.
Poiché il giorno solare è definito come l'intervallo di tempo che intercorre tra due passaggi successivi del Sole al meridiano per una data località, ovvero come il tempo che passa da quando il Sole è più alto in cielo a quando lo è nuovamente la volta successiva, l'orbita ellittica fa variare questo intervallo di tempo.
Supponiamo infatti di essere sulla Terra e di osservare il passaggio del Sole al meridiano. Dopo 23h 56m 4s la Terra ha effettuato una rotazione completa rispetto alle stelle fisse, ma poiché nel frattempo si è anche mossa sulla sua orbita deve effettuare ancora una piccola rotazione su sè stessa prima che possiamo nuovamente osservare il Sole sul meridiano. Quando la Terra si trova nei pressi del perielio questo effetto fa durare il giorno più di 24h, all'afelio meno: nel primo caso in un giorno la Terra si è spostata maggiormente sull'orbita e serve più tempo per ritrovare il Sole nella stessa posizione del cielo, nel secondo caso avviene il contrario.
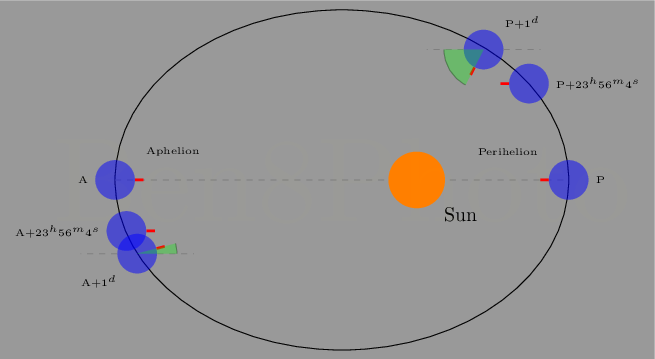
Spiegazione grafica.
Si consideri l'asta rossa come un punto sulla superficie terrestre. Al perielio la Terra si è spostata maggiormente lungo la sua orbita ed è quindi necessario un tempo maggiore affinché l'asta si trovi nuovamente di fronte al Sole. 23h 56m 4s è la durata del giorno siderale
Se si considera solamente l'eccentricità dell'orbita terrestre, allora l'equazione del tempo è in prima approssimazione una sinusoide di periodo 1 anno come in figura[3].
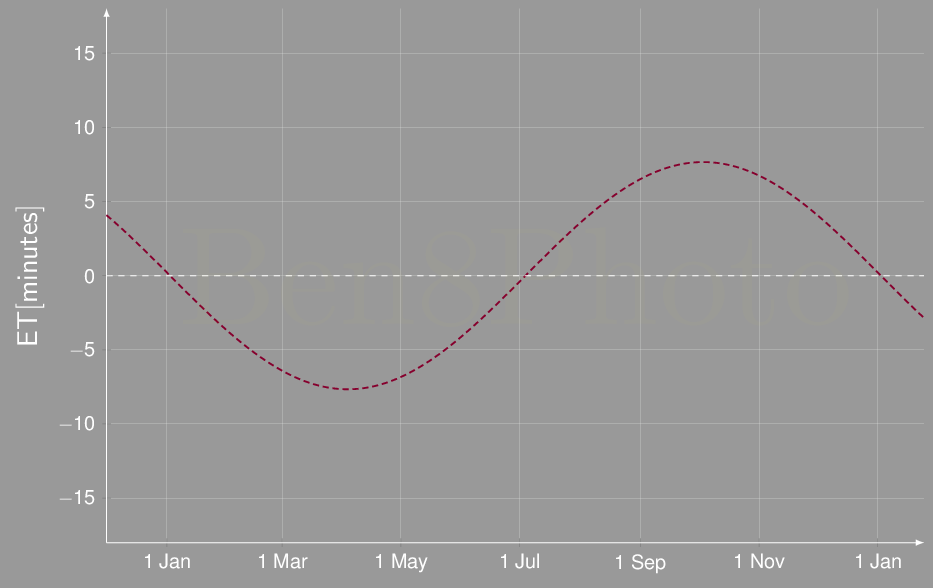
L'inclinazione
Supponiamo ora l'orbita terrestre perfettamente circolare e cerchiamo di studiare il secondo fenomeno che influisce sull'equazione del tempo. Poniamoci dal punto di vista di un osservatore sulla Terra e studiamo il moto apparente del Sole durante un anno.
Le orbite dei pianeti sono planari e la proiezione del piano dell'orbita terrestre sulla sfera celeste prende il nome di eclittica. Il Sole durante un anno visto dalla Terra compie una rotazione completa sull'eclittica.
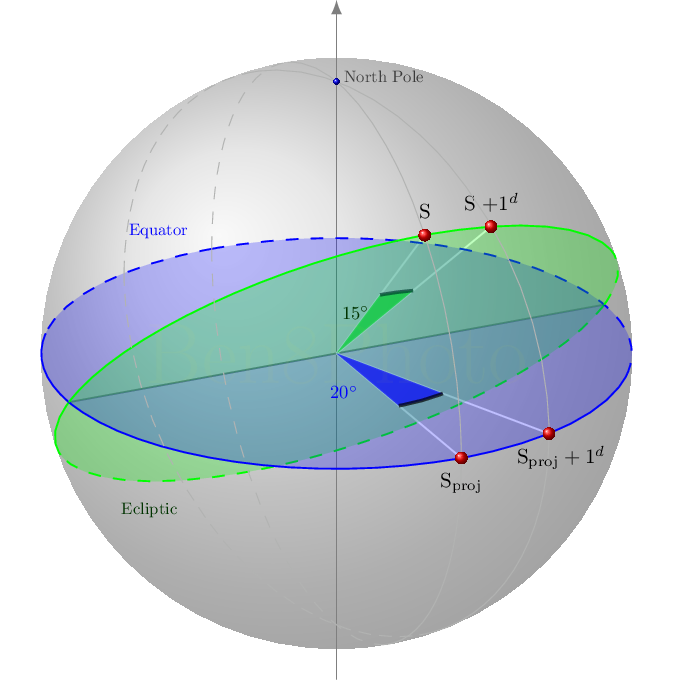
Spostamento del Sole e della sua proiezione sull'equatore celeste al solstizio
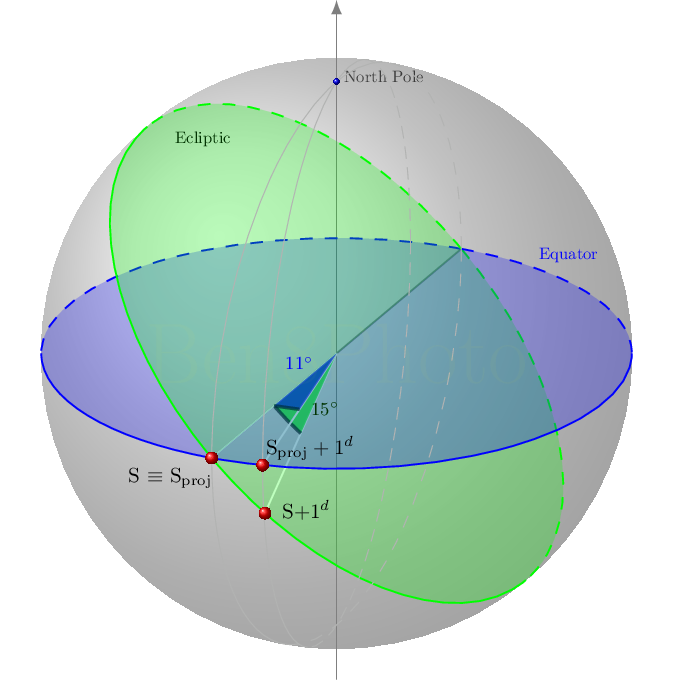
Spostamento del Sole e della sua proiezione sull'equatore celeste all'equinozio
Le due immagini rappresentano lo spostamento del Sole (S) e della sua proiezione (Sproj) sull'equatore a distanza di 1 giorno (1d). Per visualizzare meglio i vari punti si è posto lo spostamento giornaliero del Sole sull'eclittica di 15° (invece che 59') e si è aumentata l'inclinazione dell'eclittica rispetto alla realtà. Come si nota lo spostamento del Sole è uguale nelle due immagini ma lo spostamento della sua proiezione sull'equatore no.
Poiché la quantità importante che determina il mezzogiorno è l'istante in cui il Sole passa al meridiano [6] e tale istante è determinato dall'ascensione retta [7] del Sole, la quantità importante per determinare la lunghezza del giorno non è lo spostamento sull'eclittica (costante in questo modello), ma proprio lo spostamento della proiezione del Sole sull'equatore celeste. Ai solstizi, quindi, la proiezione si sposta maggiormente rispetto alla media, mentre agli equinozi di meno.
Ne consegue che la durata del giorno ai solstizi è maggiore e agli equinozi minore (l'ampiezza di questa differenza è di circa 20 secondi). L'equazione del tempo associata a questo fenomeno è una sinusoide con periodo di metà anno, come in figura [8].
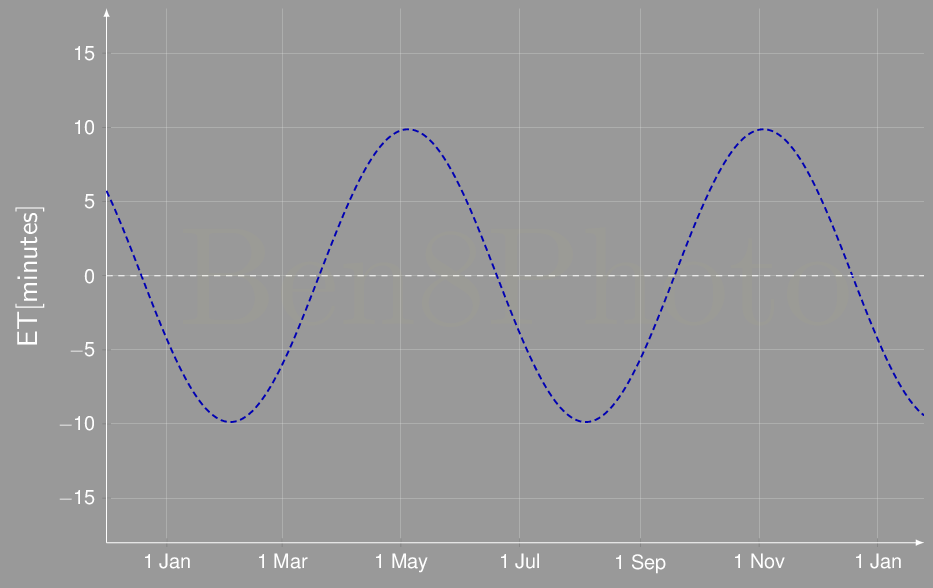
L'equazione del tempo non è altro [9] che la somma dei due grafici visualizzati precedentemente per i due fenomeni:
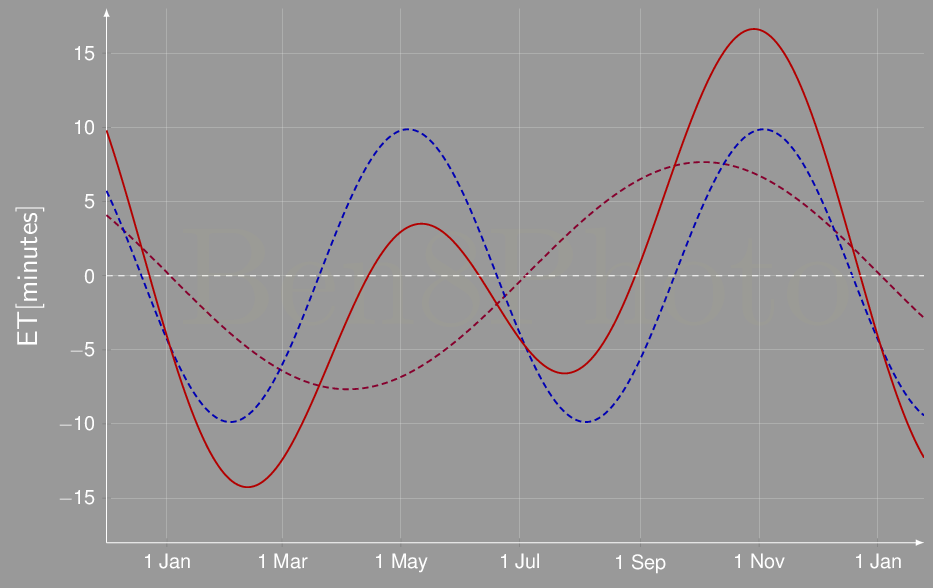
L'analemma
Ora che abbiamo capito cosa è l'equazione del tempo ci si potrebbe chiedere: perché disegnare un analemma sulla meridiana?
Si disegnano gli analemmi per poter leggere direttamente il tempo medio sul quadrante.
Infatti, in una meridiana le linee orarie diritte segnano il tempo vero, associato direttamente alla posizione del Sole, mentre se si vuole leggere il tempo medio [10] bisogna leggere l'ora sull'analemma. È per questo motivo che leggendo l'ora quando l'ombra dello gnomone si posa su una linea essa sembra sbagliata: lo scarto è proprio l'equazione del tempo di quel giorno.
L'equazione del tempo su una meridiana prende la forma di analemma in quanto la lunghezza dell'ombra dello gnomone a ora fissata indica la declinazione del Sole (e quindi generalmente due giorni dell'anno equidistanti temporalmente dai solstizi).
Il risultato è che è possibile segnare direttamente il tempo medio sulla meridiana disegnando proprio un analemma.

[1] Detto anche tempo solare apparente o semplicemente tempo solare
[2] Si sottintende che anche quella apparente del Sole è una velocità angolare come d'altronde quelle apparenti di tutti degli astri
[3] Si noti che i due momenti dell'anno in cui la Terra si trova a perielio e afelio corrispondono esattamente con gli zeri della funzione di cui vi è il grafico sopra e non con i massimi. Questo perché l'equazione del tempo è una funzione cumulativa giorno per giorno (e.g. Se oggi l'equazione del tempo è nulla e ogni giorno dura 24h 2m, allora l'equazione del tempo tra tre giorni avrà valore +6min). Il valore dello sfasamento giornaliero è quindi leggibile dal grafico come rapporto incrementale con variazione delle ascisse di un giorno. Approssimativamente lo scarto sulla durata del giorno si può quindi leggere come derivata del grafico ovvero una sinusoide con massimo e minimo proprio in corrispondenza del perielio e dell'afelio
[4] La durata reale sarebbe di 365.24 giorni. Si veda "anno tropico"
[5] Guardando l'immagine è abbastanza intuitivo che il minimo sia proprio α cosψ, al contrario può sembrare meno ovvio che il massimo è α/cosψ. Un'idea per vederlo è pensare che ai solstizi il Sole è come se si muovesse lungo una circonferenza parallela all'equatore celeste ma passante per il punto in cui si trova il Sole al solstizio. Uno spostamento su tale cerchio (non massimo) è in rapporto con lo spostamento della proiezione del Sole sull'equatore come stanno i rapporto le due circonferenze. Si vede che tale rapporto è proprio cosψ
[6] Questo è vero in generale se si considera il mezzogiorno locale e non quello segnato dagli orologi (tempo civile). Per ulteriori informazioni si cerchi la differenza tra tempo medio e tempo civile. Per le altre ore è analogo ma non si guarda il meridiano locale bensì altri meridiani a distanza di multipli di 15° da quello locale, tutti passanti per i poli
[7] L'ascensione retta di un astro e il tempo siderale, tempo calcolato unicamente sulla rotazione della Terra rispetto alle stelle fisse e quindi indipendente dalla posizione della Terra intorno al Sole, sono sufficienti a determinare quando quell'astro passa al meridiano o a qualunque angolo da esso. Per maggiori dettagli si cerchi "Ascensione retta" e "Angolo orario"
[8] Se credevi che l'ampiezza del grafico dovesse essere di 20 secondi o i massimi e gli zeri sembrano invertiti rispetto alla trattazione, allora guarda la nota [3]. L'equazione del tempo è sempre una funzione cumulativa degli scarti di cui parliamo nella trattazione.
[9] In prima approssimazione
[10] O, ancora più interessante, direttamente il tempo civile se si è costruita la meridiana considerando lo scarto in longitudine del luogo della meridiana dal meridiano terrestre scelto come principale per il tempo civile del proprio fuso orario (per l'Italia e tutti i paese con fuso +1 il meridiano 15° E)


